The Progressive Party Problem is a famous problem long thought to
be intractable for Mixed Integer Programming approaches. The problem is related to organizing a progressive party on a number of
yachts. Guest crews stay at a host boat for a few drinks and then move on to the next. The idea is to create a schedule such that
crews don't meet each other multiple times when they visit different parties. There have been several attempts to solve this model
as a MIP and the consensus conclusion was that this model could not be solved as an integer programming problem. Some successes with
constraint programming are reported. In this excersize we show that with careful modeling and a modern MIP solver we actually can solve
the model in a reasonable time on a standard PC.
You can solve this model yourself by submitting the model expressed in AMPL to the NEOS Feaspump server.
Reference: Erwin Kalvelagen, On solving the progressive party problem as a MIP, Computers and Operations Research, Volume 30, Number 11, September 2003 , pp. 1713-1726 (14)
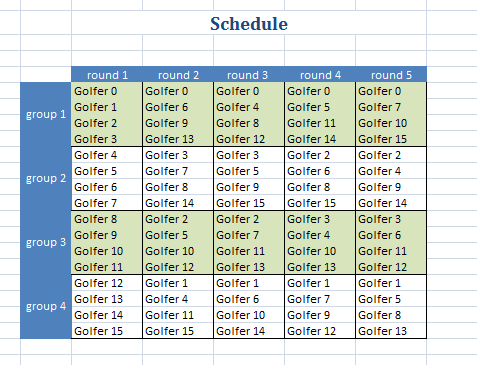
This is a related problem to the Progressive Party Problem. The original model is as follows:
can we find a schedule for 32 golf players that play in groups of four. The games are weekly
and we need an n week schedule such that each player does not play in the same group with
any other player more than once. It can be seen that n=11 is too long: by then a player
sees 3 × 11 = 33 other players. For a long time n=9 solutions are available, but
a solution for n=10 weeks was never found using integer or constraint programming.
 |
A schedule produced by Microsoft Solver Foundation |
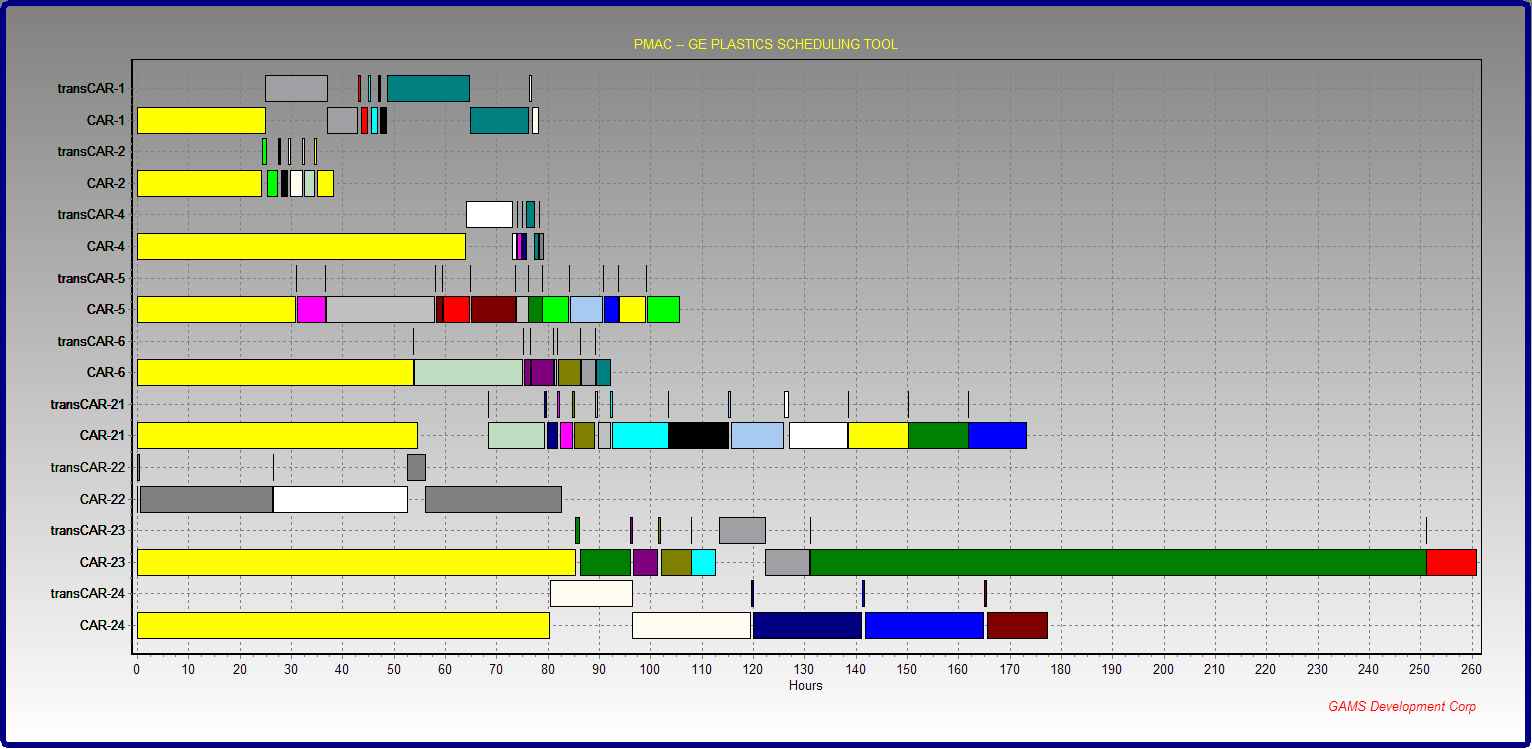The parallel machine scheduling problem with
unrelated machines and sequence dependent setup times is a challenging sequencing problem. The industrial application dealt with
scheduling jobs on extruder lines, where the setup times depent (largely) on the colors of the jobs: a white job followed by a black
job is cheaper than the other way around. The implemented model has a number of features such as optimizing per line individually before dealing
with the complete model where a MIPSTART option is used to start from a good integer solution. In addition an automatic decomposition scheme is
employed if we can detect independent subproblems (jobs can execute only on certain lines). The model employs a continuous time representation, so
no discretization is used, and no time periods are used as a variable index. The data comes from an Oracle database and
the optimizer (GAMS/Cplex) runs underneath a larger scheduling system. The GANTT charts are produced by the charting facility
of the GAMS IDE.
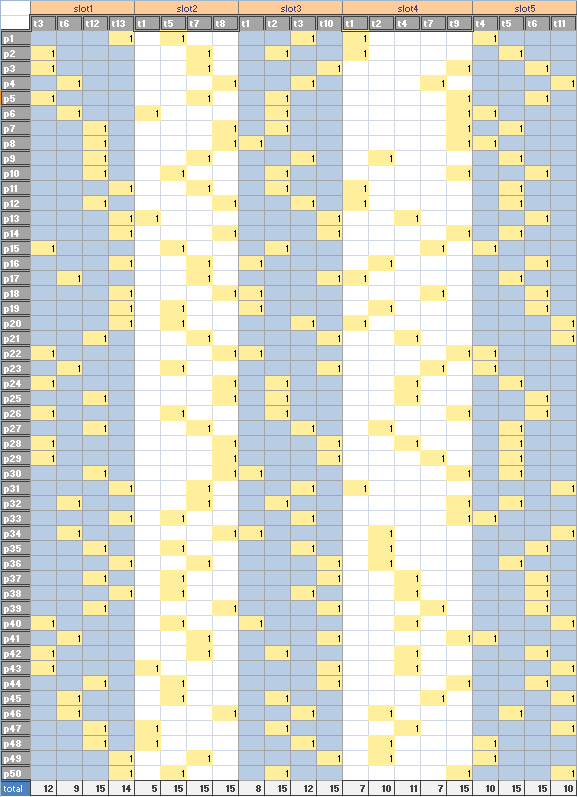A small 5-day conference is to be
scheduled such that the preferences of attendees are maximized. The problem is modeled using a standard "cube" formulation, resulting in
in a large but relatively easy to solve problem. We solve here with Cplex on four threads. The model contains the exact problem statement.
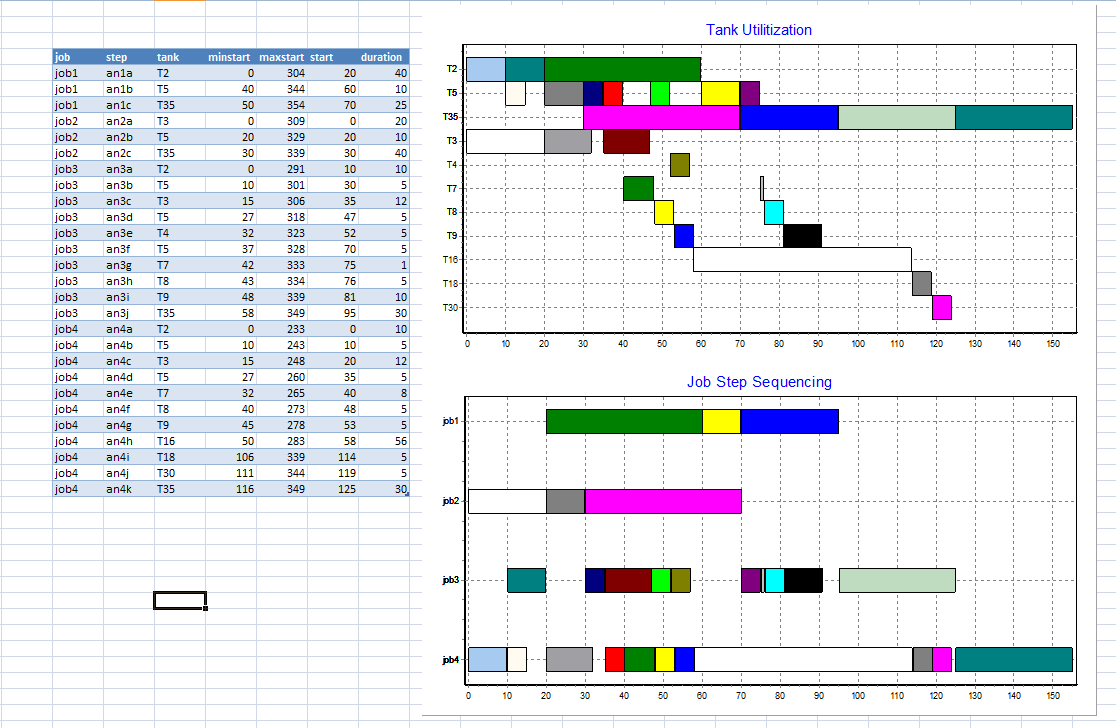
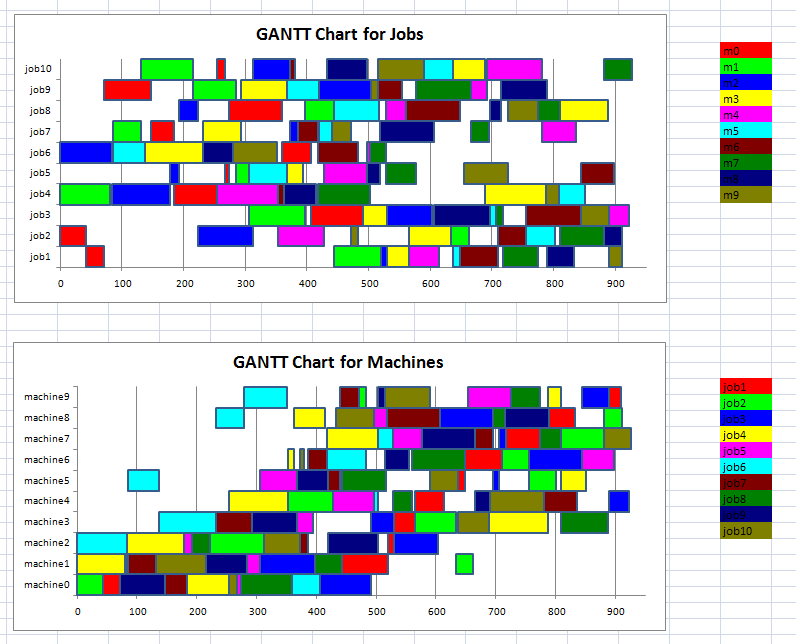Job Shop Scheduling problems can be difficult to solve. An example is ft10 with 10 jobs and 10 machines.
An optimal solution for this problem was not known for 25 years. Nowadays with the best MIP solvers
such as Gurobi and Cplex we can solve this problem formulated as a standard MIP model in less than 5 minutes.
Some VBA code has been developed to produce GANTT charts in Excel.
In practical cases, proper modeling can make a lot of difference in performance and reliability
in the solution of the optimization models.
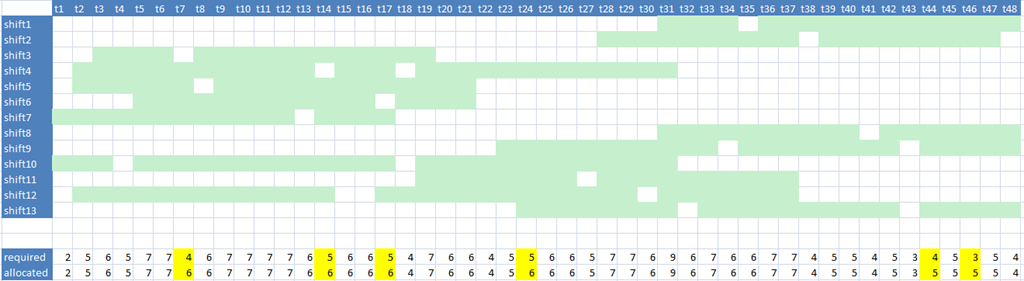For some larger problems an elegant and powerful technique called Column Generation can
be used to efficiently create near-optimal schedules. This approach has been used effectively
to generate rosters and time tables in different application areas.
