|
Many practical modeling problems have an aspect that involves statistics. In
this section we mention some documents that can help you incorporating statistical
techniques in your projects.
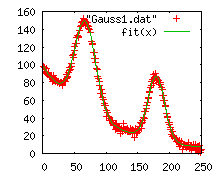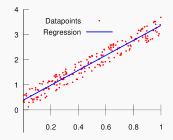
Many regression problems can also be formulated as optimization problems. However, specialized solvers may provide better performance and give more detailed output such as standard errors, covariance matrices, p-values etc. A good example is Linear Regression (OLS). There is no good way to formulate a numerically stable linear regression problem in GAMS, so for this problem the specialized LS solver can help. |
| There is no good way to express a linear regression model in GAMS. An explicit minimization problem will be non-linear as it needs to express a sum of squares. Alternatively, a linear formulation using the normal equations (X'X)b=X'y will introduce numerical instability (see example longley2.gms below). |
Therefore we have introduced a compact notation where we replace the objective by a dummy equation: the solver will implicitly understand that we need to minimize the sum of squared residuals. The GAMS/LS solver will understand this notation and can apply a stable QR decomposition to solve the overdetermined model quickly and accurately.
| The basic model will look like: |
sumsq.. sse =n= 0;
fit(i).. data(i,'y') =e= b0 + b1*data(i,'x');
option lp = ls;
model leastsq /fit,sumsq/;
solve leastsq using lp minimizing sse;
|
The fit equations describe the equation to be fitted.
| Download and documentation | ||
|---|---|---|
| Examples | ||
For more information see: http://en.wikipedia.org/wiki/Linear_regression
| In some cases we have a nonlinear statistical model to estimate: y=f(X,θ). In this case we cannot use linear algebra to find the minimizer but need to employ a numerical minimization technique. The GAMS/NLS uses NL2SOL. In addition it can use a starting point found by any of the GAMS NLP solvers. A major advantage of using GAMS is that the modeler does not have to provide derivatives. |
| Download and documentation | ||
|---|---|---|
| Examples | ||
For more information see: http://en.wikipedia.org/wiki/Nonlinear_regression.
 |
GAMS 22.8 has a few facilities to retrieve the Hessian. These examples show how this can be used to estimate variance and standard errors in some maximum likelihood estimation applications. |
|
Here are some documents that deal with statistics in a GAMS environment. They are all in PDF format. In many cases the documents contains download links to make it easier to retrieve the models. |
|
This zip file contains the GAMS/LS and GAMS/NLS regression solvers (Windows 32 bit). Note that under GAMS 22.8 LS is included. For earlier GAMS releases or for GAMS/NLS you can use this download.
