Benchmark Models

The best way to compare solvers is to try them out on your own models. However, sometimes one has to purchase solvers before the model is developed and a scaled up version of the model is available. Here we collect some large, difficult models in GAMS format that can be used to get an impression on the performance of different solvers.

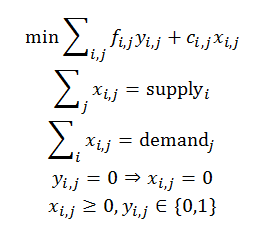
These models are on purpose somewhat artificial: that makes them simple to understand and to explain. Real world models are often more messy.

In most cases the date sets were developed to show the performance of special purpose algorithms. The current crop of state-of-the-art LP and MIP solvers can solve these problem remarkably efficiently.

Choosing Solvers

In GAMS you can choose a solver by adding MIP=CPLEX or MIP=GUROBI, etc. to the command line. This can also specified in the model as OPTION MIP=CPLEX;. If you want to run the model on multiple cores you need to add an option file. Often the easiest is to add the following code to the model: 
option mip=gurobi;
option optcr=0;
model m /all/;
m.optfile=1;
solve m using mip minimizing z;

$onecho > gurobi.opt
threads 4
$offecho

MIP: Fixed Charge Transportation Problem

This is a fairly small but difficult MIP model. In 1998 the model was largely too difficult to solve to optimality. With current state-of-the-art MIP solvers and multi-core PC's, we can solve this model in about 10 minutes.

LP: Assignment Problem

This is a fairly large assignment problem. With Cplex you can use the network optimizer to solve this very fast. Otherwise standard LP solvers also do a very good job on this, especially compared to a textbook implementation of the Hungarian Method.

Although the assignment problem is stated as a MIP, we solve as an RMIP as the binary variables assume integer values in the optimal solution automatically. As this is a network problem, it may be beneficial to select a network optimizer if available.

MIP: Job Shop Scheduling

This is a standard benchmark model that was unsolvable for 25 years. Nowadays it can be solved with standard MIP solvers. This formulation is originally from Alan Manne.

MIP: Traveling Salesman Problem

 TSP models are notoriously difficult when solved as a straight MIP. The best MIP solvers can solve problems with about 50 cities. For larger instances we can formulate more specialized algorithms in GAMS.

MIP: Plant location problems

This is a large instance of the capacitated warehouse location problem. First run whouselocdata.gms to generate capa.inc. Some Perl code is used to convert the data to GAMS input format.

MIP: Quadratic Knapsack Problem

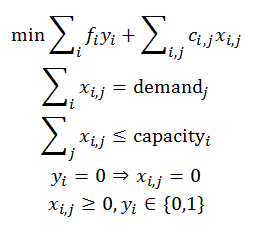
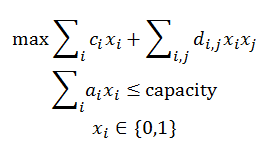
This is a large instance of the Quadratic Knapsack Problem problem. First run qkpdata.gms to generate qkp.inc. Some Perl code is used to convert the data to GAMS input format. The model linearizes the multiplication of binary variables xixj so we can solve the model with a standard MIP solver.

NLP: Convex entropy objective


This model was developed to demonstrate an issue with second derivatives in GAMS. It is based on a user model that showed poor performance. The "fast" version shows good performance with some of the interior point codes.

LP: Minimum Spanning Tree

 The problem of finding a minimum spanning tree can be formulated as a large LP.

MIP: Proving Optimality

This is a model with only 4 equations. Good MIP solvers can find very good solutions very quickly, but proving optimality takes a very long time.


MIQP: Proving Optimality

This MIQP model is quite difficult. It finds a permutation matrix such that the Frobenius norm describing the difference between two matrices is minimized. It is possible to form a linear assignment problem with the same solution. A good MIQP solver will be able to find near-optimal solutions very quickly but proving optimality is very time-consuming.


MIQP: Alternative to Dynamic Programming

This model is actually very difficult. We formulate the problem of reading a number of chapters such that each day we read a number of verses that is as close to average as possible. The MIQP formulation does not solve as easy as the Dynamic Programming algorithm.

MIP: painting by numbers

This is a puzzle where we have to paint cells black sothat clusters of back cells are formed as prescribed. The formulation from Bosch leads to large MIP's. For some examples we have troubles solving the resulting MIP.

MIP: Final MIP in column generation scheme

These are tough little models (only 26 rows by 72 or 73 columns) that take a lot of time to solve to optimality. Especially data set 2 is very difficult.

MIP: Solving large Sudokus

The best MIP solvers can solve these large Sudoku instances completely in the presolve. The iteration count will then be zero.
25 x 25 problem
81 x 81 problem

MIP: Timetabling

MIP models to create time tables can be very difficult to solve. Here are some smaller instances.

Home